
Einleitung
Albert Einstein soll den Zinseszinseffekt einst als das „achte Weltwunder“ bezeichnet haben. Ob diese Zuschreibung historisch belegbar ist oder nicht – sie unterstreicht den gewaltigen Einfluss dieses mathematischen Mechanismus auf langfristige Vermögensbildung. Wer einmal verstanden hat, wie der Zinseszins funktioniert, erkennt schnell, dass Zeit der wichtigste Verbündete des Anlegers ist.
In einer Welt, in der kurzfristige Gewinne und Spekulation oft im Vordergrund stehen, bleibt der langfristige Aufbau von Vermögen durch stetiges Investieren und Reinvestieren von Erträgen eines der effektivsten Mittel für finanziellen Erfolg. Der Zinseszinseffekt beschreibt genau dieses Prinzip: Erträge, die ein Kapital erwirtschaftet, werden nicht entnommen, sondern reinvestiert – und erwirtschaften in der Folge ebenfalls Erträge. Mit jeder Zinsperiode wird der Hebel stärker. Das Wachstum verläuft exponentiell.
Dieser Beitrag beleuchtet zunächst die mathematischen Grundlagen des Zinseszinseffekts und zeigt, warum die sogenannte Eulersche Zahl eine zentrale Rolle spielt. Anschließend werden die praktischen Implikationen aus Anlegersicht untersucht: Welche Bedeutung hat der Effekt für die private Vermögensbildung? Welche Rolle spielen Anlagedauer, Rendite und Regelmäßigkeit der Einzahlungen? Und warum ist ein früher Start so entscheidend?
Die Mathematik hinter dem Zinseszinseffekt: Was ist die Eulersche Zahl?
Der Zinseszinseffekt lässt sich mathematisch elegant durch Exponentialfunktionen beschreiben. Dabei wird angenommen, dass das Kapital kontinuierlich verzinst wird – so, wie die Seerosen auf einem Seerosenteich kontinuierlich zunehmen.
In der Finanzwelt wird dagegen in der Regel mit Zinsperioden gerechnet. Zinskupons für Anleihen werden häufig nur einmal im Jahr gezahlt, manchmal wird zweimal der halbe Kupon gezahlt, selten viermal ein Viertel des Kupons. Die zentrale Formel zur Berechnung eines Endwertes einer Investition lautet bei der Berechnung mit Zinsperioden:
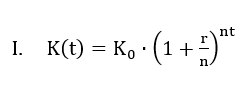
Hierbei steht:
- K(t) für das Kapital nach t Jahren,
- K0 für das Anfangskapital,
- r für den jährlichen Zinssatz,
- n für die Anzahl der Zinsperioden pro Jahr,
- t für die Anzahl der Jahre.
An einem Beispiel lässt sich die Formel gut erklären. Angenommen, wir haben ein Anfangskapital von 1000 Euro und ein jährlicher Zinssatz von 5 % wird zweimal im Jahr ausgezahlt – dann ergibt sich nach zwei Jahren ein Kapital inklusive Zinsen von:
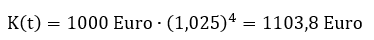
Ohne Zinseszins läge das Kapital nach zwei Jahren bei 1100 Euro, die 3,8 Euro sind mithin der – zugegeben geringe – Zinseszins. Wer jedoch 1.000 Euro über 30 Jahre zu 5 % anlegt, erhält ohne Zinseszins nur 1.500 € Zinsen (30 × 50 €). Mit Zinseszins wächst das Kapital jedoch auf über 4.300 € an – auf fast das Dreifache des Startkapitals. Dieser Unterschied zeigt die Macht der exponentiellen Kapitalvermehrung.
Schaubild 1: Wertentwicklung (1000 Euro, 5 % Zins, 30 Jahre)
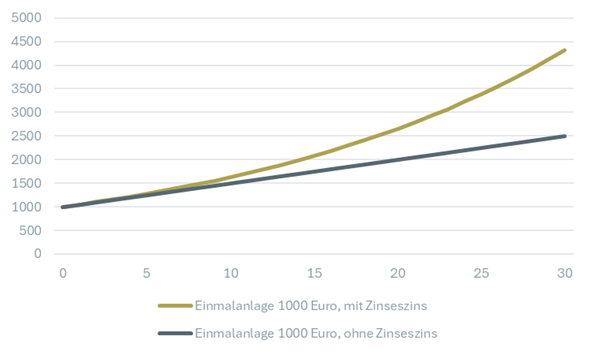
Quelle: Plutos
Wenn die Verzinsung kontinuierlich erfolgt, also ohne feste Zinsperioden, lässt sich die Entwicklung des Kapitalwerts eleganter mit Hilfe der Exponentialfunktion, d. h. mit der Eulerschen Zahl, berechnen.
Kontinuierliche Verzinsung wird beispielsweise bei Nullkuponanleihen, der Berechnung von Forward-Kursen am Devisenmarkt sowie bei der Bewertung von Optionen verwendet.
Bei der kontinuierlichen Verzinsung kommt, wie erwähnt, die Eulersche Zahl ins Spiel. Diese beträgt ca. 2,71828 und ist eine fundamentale mathematische Konstante, ähnlich bedeutsam wie π in der Geometrie. Für eine kontinuierliche Verzinsung lautet die Formel:
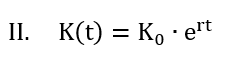
Übertragen auf unser Beispiel ergibt sich:
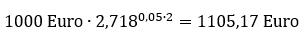
Jetzt ist der Zinseszinseffekt mit 5,17 Euro etwas größer, da wir eine kontinuierliche Verzinsung unterstellen. Anders formuliert: Bei der kontinuierlichen Verzinsung kann ein gleicher Endwert mit einem etwas niedrigeren Zins als bei der diskreten Rechnung erreicht werden.
Die Exponentialfunktion beschreibt, wie aus einem scheinbar langsamen Anfangswachstum ein rasant ansteigendes Kapital wird – vorausgesetzt, die Erträge werden immer reinvestiert.
Die Eulersche Zahl ist somit das mathematische Herzstück des Zinseszinseffekts bei kontinuierlicher Verzinsung. Auch wenn die meisten realen Anlageformen diskrete Zinsperioden nutzen, nähert sich die Entwicklung mit zunehmender Periodenzahl der Exponentialfunktion an – und wird damit zu einem beeindruckenden Instrument der Kapitalvermehrung.
Der Zinseszinseffekt aus Anlegersicht
Aus Sicht von Anlegern ist der Zinseszinseffekt weit mehr als nur ein mathematisches Konzept – er ist ein strategischer Hebel. Er zeigt, warum es nicht nur darauf ankommt, wie viel man spart oder investiert, sondern vor allem darauf, wie lange und zu welchem Zinssatz.
Drei wesentliche Einflussgrößen:
- Zeit
Zeit ist der wichtigste Faktor. Je länger das Kapital arbeitet, desto mehr greifen die exponentiellen Effekte. Frühzeitiges Investieren belohnt Geduld mit überproportionalem Kapitalwachstum. - Rendite
Bereits kleine Unterschiede im Zinssatz haben langfristig enorme Auswirkungen. Ein Unterschied von nur 1 % jährlicher Rendite kann über 30 oder 40 Jahre hinweg zu einem doppelt so hohen Endkapital führen. - Reinvestition
Der Effekt funktioniert nur, wenn Zinsen oder Erträge tatsächlich im System verbleiben und wieder angelegt werden. Dividendenausschüttungen oder Zinszahlungen, die entnommen werden, unterbrechen den Effekt.
Beispielrechnung – Ein Anleger investiert 10.000 € bei 6 % Rendite p. a.:

Je länger das Geld investiert bleibt, desto deutlicher wird der Zinseszinseffekt. Nach 30 Jahren ist das Kapital bei 6 % mehr als fünfmal so hoch – ohne dass zusätzlicher Einsatz erforderlich wäre.
Der Zinseszinseffekt funktioniert mit jeder Anlageform, die regelmäßige Erträge produziert und diese wieder investiert. Das können klassische Zinspapiere sein, aber auch Dividendenaktien, Fonds, ETFs oder Immobilienrenditen. Entscheidend ist die Disziplin des Reinvestierens und die Geduld, das Kapital langfristig wirken zu lassen.
Konsequenzen für Anleger: früher Kapitalaufbau
Wer den Zinseszinseffekt für sich nutzen will, muss vor allem eines tun: früh mit der Geldanlage beginnen.
Um den Zinseszinseffekt zu erklären, haben wir oben nur die Verzinsung eines einmal angelegten Betrags berechnet. Noch eindrucksvoller wird die Rechnung, wenn jedes Jahr oder in jedem Monat ein fester Betrag angelegt wird. Nehmen wir an, dass wir nicht nur einmal 1000 Euro anlegen, sondern jedes Jahr zusätzlich 1000 Euro anlegen. Dann ergibt sich die folgende Kapitalentwicklung:
Schaubild 2: Wertentwicklung (1000 Euro jährliche Neuanlage, 5 % Zins, 30 Jahre)

Quelle: Plutos
Denn die Zeit ist der stärkste Multiplikator im System. Genau hier liegt das größte Potenzial – wie auch die größte Herausforderung.
- Langfristige Planung lohnt sich
Wer früh startet, braucht weniger monatliche Beiträge, um das gleiche Ziel zu erreichen. - Verpasste Zeit ist schwer aufzuholen
Ein später Start kann durch höhere Einzahlungen kompensiert werden, aber nur begrenzt – die verlorene Zeit fehlt dem Kapital zum „Wachsen“. - Konstante Sparraten und Automatisierung
Wer Spar- und Investmentprozesse automatisiert (z. B. durch Sparpläne in ETFs), sorgt für Disziplin und nutzt den Effekt ohne großen Aufwand. - Zinseszins schützt vor Inflation
Langfristige, verzinste Investments schlagen die Inflationsrate meist deutlich – eine reine Bargeldhaltung hingegen verliert real an Wert.
Fazit
Der Zinseszinseffekt ist kein Mythos – er ist ein grundlegendes Gesetz der Finanzwelt. Wer ihn verstanden hat, erkennt, dass nicht Spekulation, sondern Zeit und Disziplin die wahren Hebel des Vermögensaufbaus sind. Ob mit 3 %, 6 % oder 8 % Rendite: Je länger das Kapital im System verbleibt und die Erträge reinvestiert werden, desto stärker kann das Vermögen für den Anleger wachsen.
Gerade in einer Zeit, in der junge Menschen vermehrt über Altersvorsorge, finanzielle Unabhängigkeit und nachhaltige Vermögensbildung nachdenken, sollte der Zinseszins nicht nur theoretisch bekannt sein, sondern aktiv genutzt werden.
Wer bereits mit 20, 25 oder 30 Jahren zu investieren beginnt, kann durch regelmäßige, auch kleinere Beiträge langfristig große Ziele erreichen. Wer zu lange wartet, muss mehr investieren – und bekommt oft weniger zurück.
Wichtige Hinweise:
Die in der Rubrik zur Verfügung gestellten Informationen erfolgen nach bestem Wissen und Gewissen. Informationen im Rahmen von Finanzanlagen unterliegen aber stetiger Veränderungen und wechselnder Einschätzungen. Eine Haftung wird ausgeschlossen.
Sofern in den Darstellungen Charts verwendet werden, beziehen sich diese auf den dort angegebenen vergangenen Zeitraum, die angegebene Währung und es ist angegeben, ob es sich um eine Betrachtung vor oder nach Kosten handelt. Eine Kurs- oder Wertentwicklungen in der Vergangenheit ist kein verlässlichen Indikator für zukünftige Ergebnisse. Jede Finanzanlage hat bestimmte Risiken, bitte beachten Sie die Risikohinweise.
Die Plutos Vermögensverwaltung AG ist ein kommerzieller Anbieter, die Ausführungen können daher auch werbliche und bezahlte Elemente beinhalten. Die Informationen stellen keine Anlageberatung oder Kauf- oder Verkaufsempfehlung dar, sondern sind eine Momentaufnahme der Finanzmärkte. Wir empfehlen grundsätzlich vor jeder Entscheidung die Beratung durch Ihre Bank oder einen unabhängigen Vermögensverwalter. Die Plutos Vermögensverwaltung AG erhält, sofern nicht anders angegeben, keine besondere Vergütung für die veröffentlichten Beiträge. Sofern sie aber Funktionen im Rahmen einer dargestellten Finanzanlage wahrnimmt, kann sie hierfür eine Vergütung erhalten.
Zur weiteren Information beachten Sie bitte die rechtlichen Hinweise.





